Elliptic Curves

Elliptic curves are a core foundation of modern cryptography techniques and is used extensively in web browsers, digital security products and blockchain protocols. Here we summarise the elliptic curve knowledge required for implementing verkle tries. If elliptic curves are an unfamiliar topic to you, we would suggest diving into More Reading

Elliptic curve points as a group

Using a carefully designed addition (+) operation, we can form an abelian group out of the points of an elliptic curve.

Scalar multiplication

We can extend the addition operation for elliptic curve points to define scalar multiplication:

$m*P = \underbrace{P + P + \cdots + P}_{m\ \text{times}}$, where $m$ is an integer > 0 and $P$ is an elliptic curve point.

The above expression suggests that scalar multiplication is a linear time operation. However we can use the double-and-add algorithm to execute scalar multiplication in $O(\log{N})$ time.

Multiscalar multiplication

Multiscalar multiplication is when we 'add together' several scalar multiplication results, e.g.

$m*P + n*Q = \underbrace{P + P + \cdots + P}_{m\ \text{times}} + \underbrace{Q + Q + \cdots + Q}_{n\ \text{times}}$

Elliptic curves over a finite field

We can restrict an elliptic curve such that the x and y coordinates of each point is an element of $\mathbb{F}_p$, rather than a real number $\mathbb{R}$. More formally, the continuous elliptic curve defined by

$y^2 = x^3 + ax + b$, where $x, y, a, b \in \mathbb{R}$

is restricted to

$y^2 = x^3 + ax + b\>(mod\>p)$, where $x, y, a, b \in \mathbb{F}_p$ and $p$ is a prime number

This transforms the graph from a continuous curve to a discrete set of points.

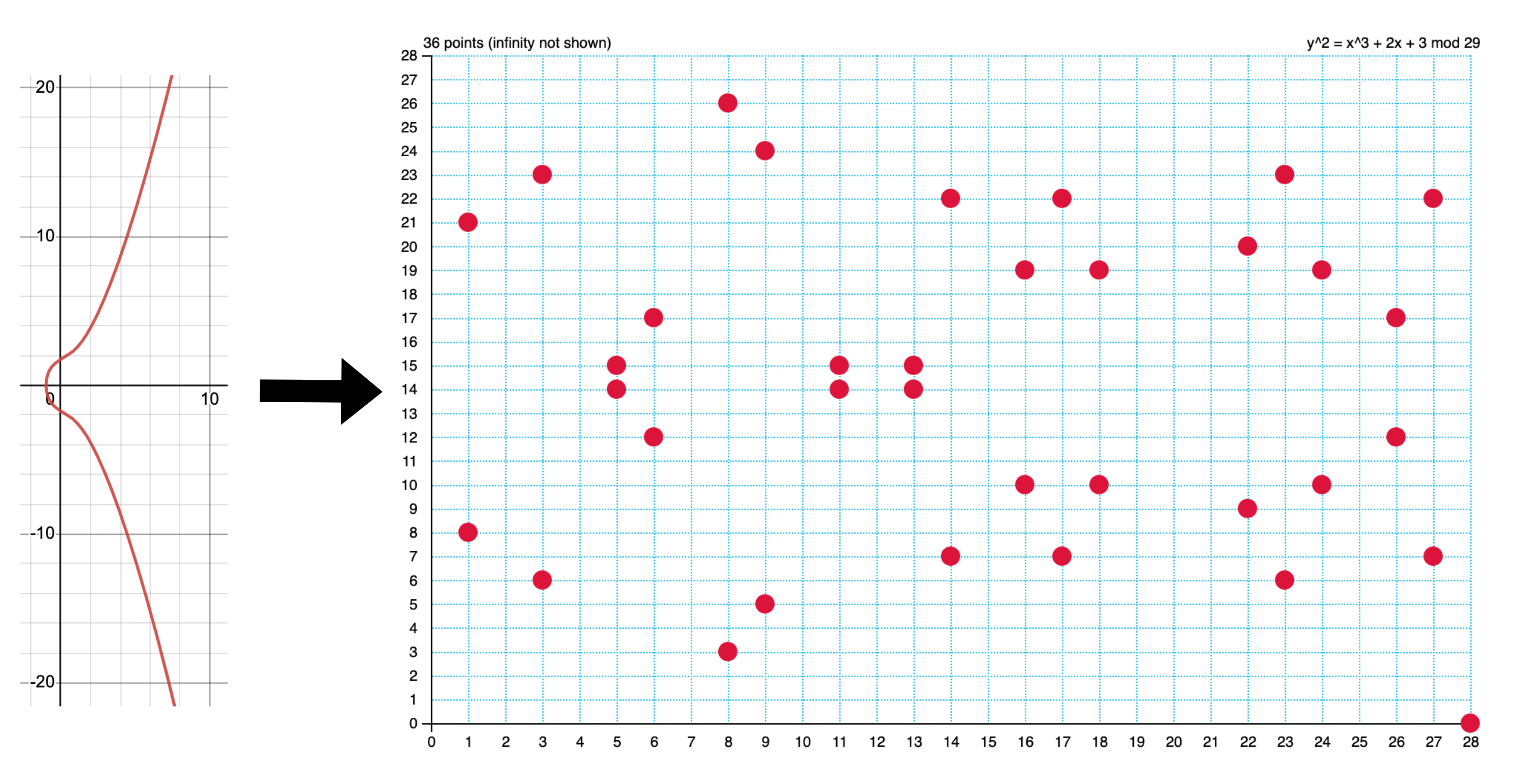Figure 1. Elliptic curve defined by $y^2 = x^3 + 2x + 3$ transformed from being defined over $\mathbb{R}$ to $\mathbb{F}_{29}$

The important mathematical result here is that elliptic curve points over a finite field still form an abelian group.

Elliptic curve discrete logarithm problem (ECDLP)

For the scalar multiplication $Q = n*P$

Where $P$ is an elliptic curve point over $\mathbb{F}_p$, $n$ is a scalar $\in \mathbb{F}_p$ and $Q$ is the scalar multiplication result (also an elliptic curve point over $\mathbb{F}_p$ by the group property of closure).

• Given $n$ and $P$, it is 'easy' to find $Q$ => Scalar multiplication, known $O(\log{N})$ algorithm
• Given $Q$ and $P$, it is 'hard' to find $n$ => Discrete logarithm problem, exponential time algorithms for the general case

This mathematical result forms a trapdoor function, and is a core security assumption of applications using elliptic curve cryptography.

The ECDLP is a 'harder' problem than the general discrete logarithm problem (DLP) in the sense that the fastest known general-purpose algorithm for the ECDLP has an exponential time complexity, whereas the fastest known general-purpose algorithm for the DLP has a subexponential time complexity. Hence cryptographic keys based on ECDLP can be significantly smaller than keys based on DLP, and still be more secure.

Elliptic curve forms

Elliptic curves can be mathematically expressed in multiple forms - Weierstrass, Montgomery and twisted Edwards forms are commonly used in cryptographic applications. The $y^2 = x^3 + ax + b$ where $a, b \in \mathbb{F}_p$ expression we have previously referred to represents the Weierstrass form.

Montgomery form ($by^2 = x^3 + ax^2 + x$, where $a, b \in \mathbb{F}_p$) and twisted Edwards form ($ax^2 + y^2 = 1 + dx^2y^2$, where $a, d \in \mathbb{F}_p \setminus \{0\}$) are frequently preferred in practical software implementations because addition and scalar multiplication operations are more efficient, and Weierstrass form implementations suffer from vulnerability to side-channel attacks.

Every Montgomery form curve can be transformed into a mathematically equivalent twisted Edwards form curve, this relationship is known as birational equivalence. However over the finite field $\mathbb{F}_p$, not every Weierstrass form curve can be transformed into a twisted Edwards curve - only a small subset of Weierstrass curves can be transformed into a twisted Edwards curve in $\mathbb{F}_p$.

More Reading

• Elliptic Curve Cryptography: a gentle introduction
• A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography - Cloudflare
• An Introduction to the Theory of Elliptic Curves - University of Wyoming